マルコフ性、マルコフ過程、マルコフ報酬過程、マルコフ決定過程

　マルコフ決定過程（MDP）を勉強する上では、１つずつマルコフ過程から少しずつ変数を増やして理解していくのが分かりやすい様な気がします。[1]がそのパターンでしたので、[1]のほぼ流用の形でマルコフ決定過程についての紹介をしたいと思います。

マルコフ性
マルコフ過程
マルコフ報酬過程
マルコフ決定過程

マルコフ性（Markov Property）

　マルコフ性とは、次の状態は現在の状態のみに依存し、現在より前の状態（過去の状態）には依存しないという性質のことです。例えばサイコロを振る時、何回かサイコロを振っていたとしても、出る目は過去に依存しないですよね？そういうことを指します。

f:id:graziegrazie:20190601223856p:plain — Fig. 1 Markov Property[1]

　状態が複数ある場合、その遷移確率は行列で表現できます。行列で表現すると言うと小難しく聞こえますが、A -> B, B -> C, A -> C...というのを総当たり表の様に記載しただけです。なお"確率"と言うだけあって、状態Aから次の状態へ遷移する確率の和（状態遷移行列の行成分の和）は1になります。

f:id:graziegrazie:20190601225101p:plain — Fig. 2 状態の遷移確率[1]

-
マルコフ過程（Markov Process, MP）

　マルコフ過程とは、マルコフ連鎖とも呼ばれ、タプル $\langle S, P \rangle$ で表現されます。ここで、 ${S}$ は状態の集合、 ${P}$ は状態遷移確率の行列をそれぞれ表します。例えばFig. 3のように状態遷移表と状態遷移行列で表現できます。確率については、計算式で求められることもあるのでしょうが、実験的に求めることが多いと思います。データを蓄積する過程で、状態遷移確率は適宜更新されます。行成分の和が１になることも確認してください。

f:id:graziegrazie:20190601230334p:plain — Fig. 3 マルコフ過程[1]

-
マルコフ報酬過程（Markov Reward Process, MRP）

　マルコフ過程に報酬という概念を加えたもので、タプル $\langle S, P, \textbf{R}, \boldsymbol{\gamma} \rangle$ で表現されます。ここで ${\textbf{R}}$ は報酬、 ${\boldsymbol{\gamma} \in \lbrack 0, 1\rbrack }$ は割引率と呼ばれます。最終的に最も高いreturnを稼げる（最も褒められる）状態遷移シーケンスを見つけることが目的です。予想されるreturnは、Fig. 4の様にして求められます。将来に得られるだろう報酬に関しては、割引率が掛けられていることがポイントです。未来の報酬というのは現時点では不確かなもので、得られない可能性があります。そのため確実に得られる直近の報酬はそのままで、将来的な報酬は先であればあるほど、その価値を低く（割り引いて）考えます。

f:id:graziegrazie:20190602003028p:plain — Fig. X Markov reward process[1]

f:id:graziegrazie:20190602041740p:plain — Fig. 4 Formula of return calculation[1]

報酬を考慮した時の状態遷移表は下記Fig. 5の様に表現されます。

f:id:graziegrazie:20190602041859p:plain — Fig. 5 Markov reward process[1]

-
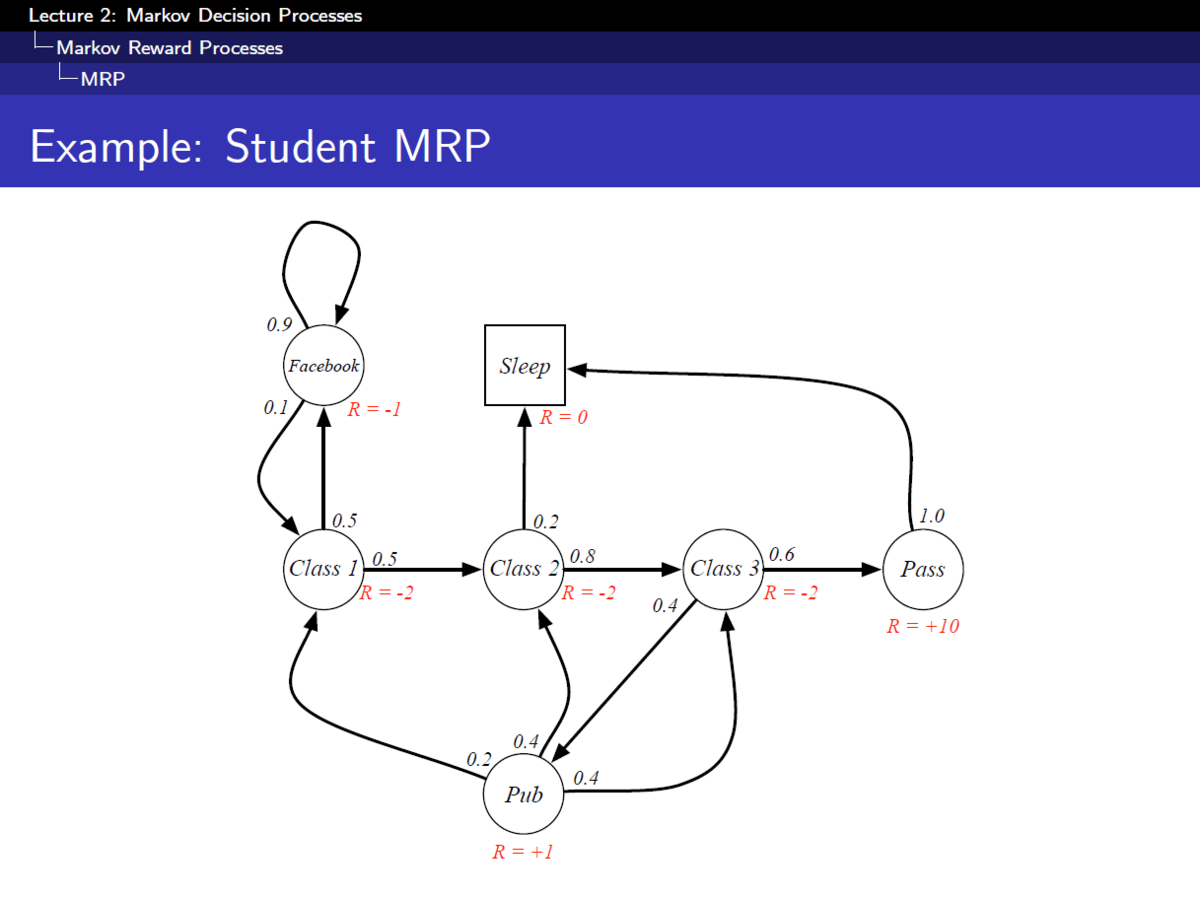
マルコフ決定過程（Markov Decision Process, MDP）

　マルコフ報酬過程に対し、行動という概念を加えたものです。状態遷移という結果が勝手に起こる訳ないので、原因である行動（事象が正しい場合もあると思います）を考慮することは大変合点がいきます。どの行動をとるかについても、状態遷移と同様に確率で表現されます。ただし行動は現在の状態を元に決定されるため、その行動に関する確率は状態を使った条件付き確率で表現されます。この確率はPolicyと呼ばれます。Aさんはこういう時にこうする、というものを表現している訳なので、意味合いとしては納得しやすい様に感じます。