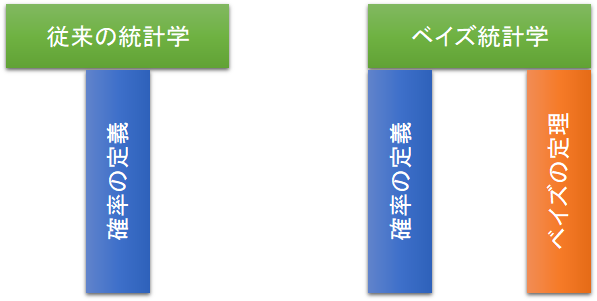
従来の統計学とベイズ統計学の違い
- 従来の統計学
- データについての不確実性を確率で表現・推論する統計学
- データが少ないと使い勝手が悪い
- パラメータや仮説の不確実性を確率で表現・推論する統計学
- データ数に依らず議論が可能
イメージとしては下図のようになる。
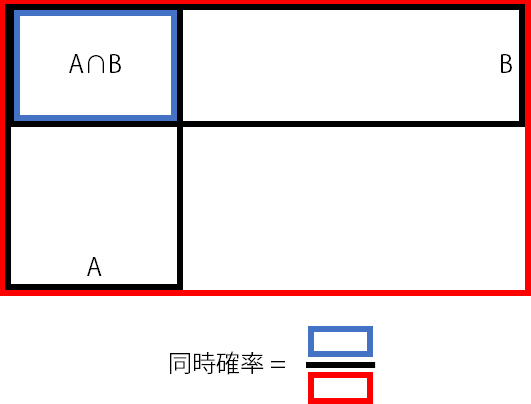
乗法定理
同時確率を条件付き確率の積で表せる。例えばN回目の確率はN-1回目の確率を使って表現できる。これを図で示すと下図のようになる。
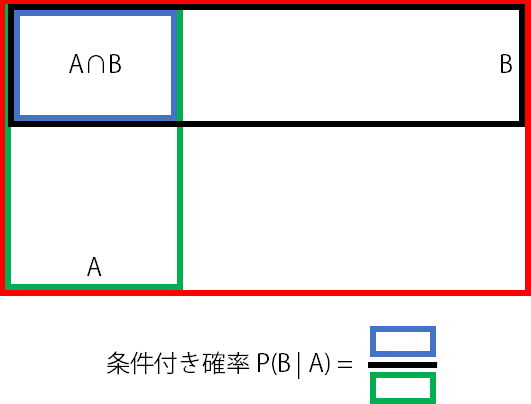
ベイズの定理
図に表すと下記の通りで、Bを基準に考えていた確率を、Aを基準に考え直すことができる。ベイズの定理を日本語で表すと、
だが、これをと置き換えると、
とできる。
例題1.
4/1が晴れ, 曇り, 雨の確率はそれぞれ0.3, 0.6, 0.1であり、4/2が雨の確率は、4/1が晴れ, 曇り, 雨の時それぞれ0.2, 0.5, 0.4とする。このとき、4/2が雨でかつ4/1が曇りの確率を求めよ。
ベイズの定理を使うコツ=とにかく分解すること
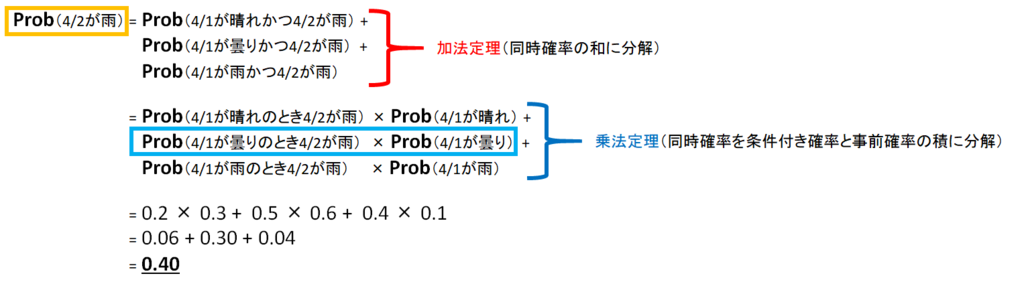
従って求める確率は

となる。分母の値(データが得られる確率)が直接与えられない場合は、このようにして求める。
|
|
理由不十分の原則
確かな情報がない場合は、適当な値をセットできる
ベイズ更新
新旧データ或る時に、旧データから得られた事後確率を新データの事前確率として利用すること
例題2.
ケンの彼女K子がケンを好きな確率は?
この問題では、心を確率モデル化してみる。心には2種類の因子があり、それらを「愛」・「憎」とする。このとき、
| K子の心情 | 嫌い | ふつう | 好き |
|---|---|---|---|
愛 |
1 |
2 |
3 |
憎 |
3 |
2 |
1 |
デートの印象が悪い → 「憎」が引かれた
デートの印象が良い → 「愛」が引かれた
*引かれた「愛」・「憎」は元に戻る。つまりそれぞれの感情において、「愛」・「憎」の数は常に一定とする。
最近2回のデートの印象は、順に「良」・「悪」であったとする。
1回目のデートで良を得る確率
D=1回目のデートで良を引く
H=K子がケンを好き
|
|
K子がケンのことが好きかの事前情報はないので、理由不十分の原則から「好き」・「ふつう」・「嫌い」は各1/3の確率とするのが一般的である。しかしケンはK子と直に接していることから、ケンの実感を採用することが出来る。これは明確な根拠がないため、各心情である確率をを1/3するよりもケンの経験を根拠にしていることから、精度は高そうである(勿論本人が勘違いをしている可能性は捨てきれないが。。。)。このようにベイズ確率では、経験のような根拠の薄い情報を考慮できるという柔軟さがある。
その結果、
事前準備
1回目のデートの結果を踏まえ、
をそれぞれ求める。結果は、
| 嫌い | ふつう | 好き |
|---|---|---|
| 0.04 | 0.24 | 0.72 |

よって2回のデートの結果、K子がケンに対して抱いている感情は、
確率分布
例題3.
表の出る確率がのコインがあり、3回投げると
- 1回目 表
- 2回目 表
- 3回目 裏
と出た。この時の確率分布を求めよ。
この場合、データは「表」が出ること、仮説は「表」の出る確率がとなる。よって求める確率は、
ここで"「表」の出る確率が"という文言を"
のコイン"と置き換えると、上記は
ベイズの定理の左辺は原因が発生する確率
は定数のため
と置く
- 尤度 :
- 事前確率:1(理由不十分の原則)
よって
となる。
より、
となる。2回目の事後分布は、
1回目と同様にしてとなる。3回目は裏が出たので、
であり、
*参考文献
「頻度論」の学者と「ベイズ論」の学者が対談したら | 『統計学が最強の学問である[実践編]』発刊記念対談 | ダイヤモンド・オンライン