ROSでcompressed imageをdecompressする方法(コマンドライン)
- Image
rosrun image_transport republish compressed in:=/camera/image_raw raw out:=/camera/image_raw
- Depth
rosrun image_transport republish compressedDepth in:=/camera/image_raw raw out:=/camera/image_raw
gitの使い方
git submodule
レポジトリに対し、別のレポジトリを関連付けるためのコマンドです。例えばhogeというレポジトリがあるとして、そのレポジトリに対して
git submodule add https://xxx.fuga.git
とすると、hogeレポジトリに
fuga@8fc2cdb
が登録されます。上記8fc2cdbは、hogeに関連付けたfugaのコミットコードです。これにより、hogeレポジトリがfugaレポジトリのどのコミットを利用しているかが明示できます。加えて、hogeをcloneなどした時に、fuga@8fc2cdbも取得できるようになります。
Gazebo上のPR2をMoveIt! + Teleopで動かす
Gazebo上のPR2のEnd-Effectorを動かしたいと思い。その方法について検討しました。その結果、MoveIt!を利用することにしました。MoveIt!はIKを解く必要があるので、End-Effectorの目標座標を与える必要があります。手入力で与えるのは面倒なので、ゲームコントローラでTeleoperationすることにし、実際にできました。その結果を纏めたいと思います。
# 実行した環境
# 実行手順
最初は既存のプログラムを実行すればOKです。
- roslaunch pr2_gazebo pr2_empty_world.launch
- roslaunch pr2_moveit_config move_group.launch
- roslaunch pr2_moveit_config moveit_rviz.launch config:=true
これらを実行した後、RViz上でInteractive Markerを動かしてPlan & Executeすれば、markerと同じ姿勢にPR2が動作します。私は"Approx IK Solution"にチェックを入れ、かつCollision-aware IKをオフにして実行しました。MoveIt!のIKのための目標座標は、jsk_teleop_joyを使いました。ただ、デフォルト設定のままだと下記のような問題点・不都合があるので、それぞれ下記のように対応した。
- コントローラの設定が、既存のものだと対応していない可能性がある → 自分が使いたいコントローラに合わせてコントローラのstatusの追加が必要
- frame_idが/odom_combinedになっていて、End-Effectorをちょっと動かそうにも基準がodom_combinedになっていて、直感的に目標位置を合わせづらい → frame_idを、r_write_roll_linkなどに変更
ROSでstatic_transform_publisherを使うならばtf2_rosの方を使うのがよい
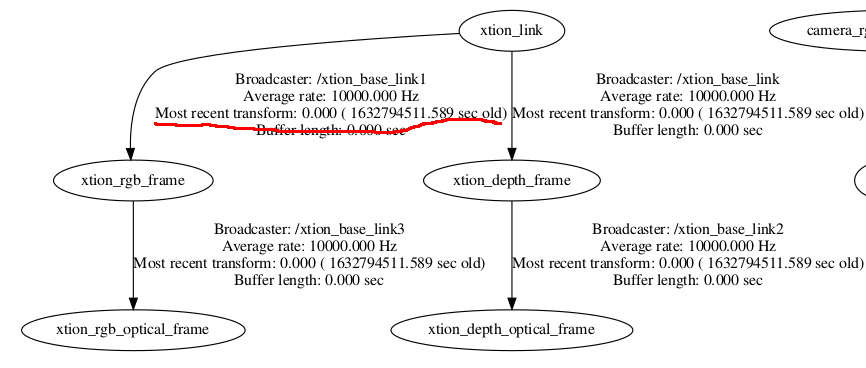
ROSでtfのstatic_transform_publisherを使うと、[1]に記載のように、未来のtime stampが発生し、トラブルがおきたことがありました。tf2の(パッケージ的にはtf2_rosの)static_transform_publisherは、フレームレートを決める必要がありません([2]の1.5参照)。そのため、Fig. 1のように、発行時刻がt=0となり、以降は更新されないので、time stampによる問題が発生しません。みなさん、なるべくtf2を使ったほうがよさそうです。
ROSネットワークの環境変数設定用スクリプト
表記のスクリプトを書いてみました。参考になれば幸いです。
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
- -
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
#!/bin/bash
# this script sets ROS network related environemt variables, ROS_IP and ROS_MASTER_URI
IP_ADDR=`ip addr show enp0xxxx | grep "inet\b" | awk '{print $2}' | cut -d/ -f1`
if $IP_ADDR ; then
export ROS_IP=$IP_ADDR
export ROS_MASTER_URI=http://$(getent hosts nxo | cut -d' ' -f 1):11311
else
echo "No Ether IP address detected!"
fi
# this case ethernet is used. if enp0xxx is replaced another device such as wlp0xxx, this script is used for it.
-
-
-
-
-
-
-
-
- -
-
-
-
-
-
-
-
#!/bin/bash
# following script unset ROS network related environment variables
export ROS_MASTER_URI=http://localhost:11311
unset ROS_IP
ROS in python + 仮想環境でpip installしたはずのモジュールがModuleNotFoundになる
ROSのpythonコードを実行するとき、仮想環境下で実行することが多いと思います。このとき、rosrunでコードを実行しようとすると、venv下のpythonのsite-packagesにpathが通っておらず、ModuleNotFoundになると思います。ただ、python xxx.pyのようにすれば、トラブルなくコードを実行できると思います。これは、pythonを実行すれば仮想環境下のsite-packagesにパスが通っているものの、rosrunだとROS環境下で定義された探索パスを使うことが原因です。そのため、下記の3つの呼び出し方で、それぞれsys.pathの中身を比較してみました。なお、今回はmycobot_rosというROSパッケージを使った時のログを使って示します。
- rosrun aaa xxx.py
- python3 xxx.py
- ./xxx.py (xxx.pyをchmod 777で実行権限を付与)
rosrun aaa xxx.py
['/home/user/catkin_ws/devel/.private/mycobot_communication/lib/mycobot_communication', '/home/user/catkin_ws/devel/lib/python3/dist-packages', '/opt/ros/noetic/lib/python3/dist-packages', '/usr/lib/python38.zip', '/usr/lib/python3.8', '/usr/lib/python3.8/lib-dynload', '/home/user/.local/lib/python3.8/site-packages', '/usr/local/lib/python3.8/dist-packages', '/usr/lib/python3/dist-packages']
python3 xxx.py
['/home/user/catkin_ws/src/mycobot_ros/mycobot_communication/scripts', '/home/user/catkin_ws/devel/lib/python3/dist-packages', '/opt/ros/noetic/lib/python3/dist-packages', '/usr/lib/python38.zip', '/usr/lib/python3.8', '/usr/lib/python3.8/lib-dynload', '/home/user/catkin_ws/src/mycobot_ros/venv/lib/python3.8/site-packages']
./xxx.py
['/home/user/catkin_ws/src/mycobot_ros/mycobot_communication/scripts', '/home/user/catkin_ws/devel/lib/python3/dist-packages', '/opt/ros/noetic/lib/python3/dist-packages', '/usr/lib/python2.7', '/usr/lib/python2.7/plat-x86_64-linux-gnu', '/usr/lib/python2.7/lib-tk', '/usr/lib/python2.7/lib-old', '/usr/lib/python2.7/lib-dynload', '/home/user/.local/lib/python2.7/site-packages', '/usr/local/lib/python2.7/dist-packages', '/usr/lib/python2.7/dist-packages']
(先頭に、#!/usr/bin/env python2、というshebangを追加しています)
上記のように、確かに仮想環境化でrosrunしても、venvの下のsite-packagesにパスが通っていないことが確認できました。sys.path.appendにvenv下のsite-packagesの絶対パスを登録すれば、今回のエラーは回避できます。もっとキレイな方法があれば、教えていただけますと幸いです。
MyCobot(実機)をROSで動かす
中華製の格安だけどそれなりの性能を誇るロボットアームMyCobotですが、アジャイル的に開発しているようで、システム構成や動作手順がコロコロ変わっており、過去例がなかなか参考にならないという難点があります。そこで、2021年11月28日現在で私がsliderでmyCobotを動かした手順を記録しておきます。何かの参考になりましたら幸いです。
環境
ROSでの動作手順
動かすまでの事前準備については、elephant roboticsが提供するmyCobotのマニュアルを参照してください。環境構築が終わったら、まずmyCobotに電源と通信用のUSBケーブルを接続します。接続後、basicの画面が点けば、正しくFirmwareが書き込まれており、myCobot実機が動作する状態になっています。次に、basicの画面上でTransponderを選択してください。そして
roslaunch mycobot_280 slider_control.launch
を実行し、RVizとスライダーを立ち上げてください。次に、RViz上のmyCobotとmyCobot実機を同期させるために、
rosrun mycobot_280 slider_control.py
を実行してください。上記を実行すると、実機とRVizで姿勢の差異があると、実機はRvizと同じ姿勢になるべく早く動こうとします。この時何も確認など行われないので、実機近くに障害物など置かないように注意してください。
簡単ではありますが、以上がmyCobot実機を動かす手順です。細かな部分は省略しているので、不明点があればご質問いただければ幸いです。
