gggggraziegrazie

graizegrazieさんのやったこと、学んだことを記録する雑記帳です

Dockerで０からコンテナ接続までのコマンドの流れを図にしてみた

Docker初心者のため、どのコマンドを使えばどうなるかの関係がイマイチ覚えづらいです。また少し使った後にしばらく間が空くと、完全に流れを忘れてしまうのが悩みでした。そこで流れを図にしてみました。今回の対象は、pull, build, create, run, start, stop, attach, execです。

f:id:graziegrazie:20180715162406p:plain
図. Dockerでのコマンドフローのイメージ

間違っていたり、付け加えた方がよい情報などありましたら教えていただけますと幸いです。

NDT( Normal Distributions Transform )

　NDT[1]とは、２つの点群のマッチングをさせる手法の１つです。点群マッチングとは、ある点群（参照点群と呼ぶ）に対し、ある点群（入力点群と呼ぶ）がどれだけ重なっているか、重ねるためには点群をどの様に移動させるべきかを判断するための手法です。点群マッチングの手法としては、他にICP(Iterative Closest Point)があります。ただしICPは、入力点群の各点が参照点群に対してどれだけ離れているかを計算する必要があります。そのため、入力点群の数が多くなるほど計算量が増えるという問題があります。
　これに対してNDTは、ボクセルやグリッドを使って点群が存在する空間を等間隔に分割するし、ボクセル又はグリッド毎に求めた正規分布を使って点群の表現、マッチングを行うため、計算量を削減することができます。正規分布の計算方法は下記の通りです。
①各ボクセル又はグリッド毎に、点群の平均座標を求める
②求めた平均座標を使い、共分散行列を求める
③この平均座標と共分散行列を元に、点群を正規分布で表現する

イメージとしては、下記のスライドと画像が参考になるかと思います。
https://camo.qiitausercontent.com/f07fa661da685d0d6f45f1650c7737b2a0b80547/68747470733a2f2f71696974612d696d6167652d73746f72652e73332e616d617a6f6e6177732e636f6d2f302f3133313535382f33333136356235392d653038622d333861622d666338302d3464623362323163613562382e706e67
このスライドはソースはここ
そしてスライドの大元のソースはここ

f:id:graziegrazie:20180701000424p:plain
出典：田窪ら, "高解像度NDTグリッドマップを用いた環境地図生成", 日本機械学会論文集（C編）78巻793号, 2012

点群のマッチングは、

  • p = (t_x, t_y, \theta)^T: 入力点群の座標系から見た参照点群の座標系の相対座標。
  • T(p): 入力点群座標系から参照点群座標系への変換行列
  • x_i: 入力点群中の点iの座標（生データ）。
  • x^{'}_i: 入力点群を参照点群の座標系に変換した後の入力点群中の点iの座標。つまり、 x^{'}_i = T(p) x_i。
  • \Sigma_i, q_i: 変換後の入力点群{x^{'}_i}の共分散と平均座標。共分散と平均は各ボクセル又はグリッド毎に計算することに注意。

このとき、下記の関数score(p)を使って点群同士がどれくらいマッチングしているかを評価する。
f:id:graziegrazie:20180701003934p:plain
出典:[1]

SLAM等のアプリケーションでNDTを使い、この評価関数の値が低い場合は、参照点群と入力点群が重なる（つまり地図と現在得た点群がマッチする様に調整し、自己位置を見つける）ように、pの位置を調整していく。調整アルゴリズムについては[1]を参照のこと。

参考文献

[1]P. Biber and W. Strasser, "The normal distributions transform: a new approach to laser scan matching," Proceedings 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2003) (Cat. No.03CH37453), 2003, pp. 2743-2748 vol.3.

install scikit-sparse on win7(halfway)

コレスキー分解をWindowsのPython環境で使いたかったので、上記を試してみました。pip install自体は通ったのですが、目的であるコレスキー分解はまだ動いていませんが。。。

構築環境

手順

1. このページからzipをダウンロード
＊pip install scikit-sparseとしてもよいのですが、後程出てくるglobal-optionを使っている間に、なぜかzipからのインストールにしてしまいました。。

2. このページを参考にscikit-sparseに必要なSuiteSparseのコンパイル

3. python -m pip install -e scikit-sparse's_directory_path --global-option=build_ext --global-option="-ICHOLMOD's_header_path;SuiteSparse's_header_path" --global-option="-LSuiteSparse's_lib_file_path" --global-option="-lsuitesparseconfig metis amd btf camd ccolamd colamd cxsparse klu ldl spqr umfpack liblapack libblas"
斜体の部分は適宜自分の環境にあったパスに変えてください

＊pipを使ってファイルからモジュールをインストールする際の方法はこちらを参考にしてください。
＊global-optionについては、ここを参考にしてください。

ただこれだけだと、scikit-sparseのimport(import sksparse)は可能ですが、"from sksparse import cholsky"は出来ませんでした。

"図解・ベイズ統計「超」入門 あいまいなデータから未来を予測する技術"を読んで

数学

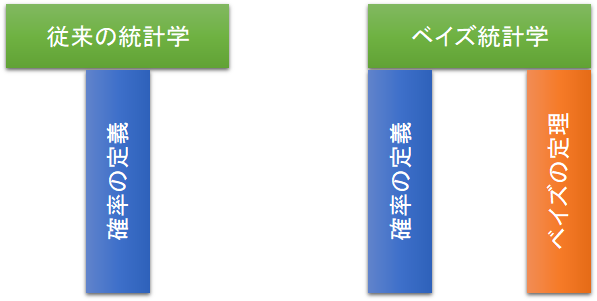
従来の統計学とベイズ統計学の違い

　- データについての不確実性を確率で表現・推論する統計学
　- データが少ないと使い勝手が悪い

　- パラメータや仮説の不確実性を確率で表現・推論する統計学
　- データ数に依らず議論が可能

イメージとしては下図のようになる。

Fig. 従来の統計学とベイズ統計の違い

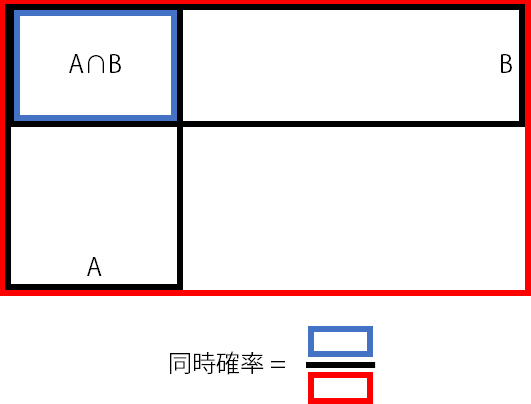
乗法定理

同時確率を条件付き確率の積で表せる。例えばN回目の確率はN-1回目の確率を使って表現できる。これを図で示すと下図のようになる。

f:id:graziegrazie:20171011225817p:plainf:id:graziegrazie:20171011231252p:plain
Fig. 確率のイメージ図(left:同時確率、right:条件付き確率)

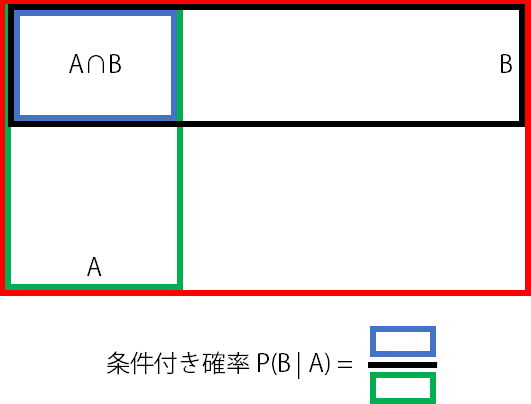
ベイズの定理

図に表すと下記の通りで、Bを基準に考えていた確率を、Aを基準に考え直すことができる。ベイズの定理を日本語で表すと、
{ \displaystyle 「Bが起こった時にAの起こる確率」＝ \frac{「Aが起こった時にBの起こる確率」\times「Aの起こる確率」}{「Bの起こる確率」} }
だが、これを{ \displaystyle A=仮説、B=データ}と置き換えると、
{ \displaystyle 「データを得られた時に仮説が成立する確率」＝ \frac{「仮説の元でデータが生じる確率（尤度）」\times「仮説が生じる確率（事前確率）」}{「データが得られた確率」} }
とできる。

f:id:graziegrazie:20171016235411p
ベイズの定理

例題1.

4/1が晴れ, 曇り, 雨の確率はそれぞれ0.3, 0.6, 0.1であり、4/2が雨の確率は、4/1が晴れ, 曇り, 雨の時それぞれ0.2, 0.5, 0.4とする。このとき、4/2が雨でかつ4/1が曇りの確率を求めよ。

{ \displaystyle Prob(4/2が雨の時に4/1が曇り) = \frac{Prob(4/1が曇りの時に4/2が雨) \times Prob(4/1が雨) }{Prob(4/2が雨)} }

{ \displaystyle Prob(4/2が雨) = \frac{Prob(4/1が曇りの時に4/2が雨) \times Prob(4/1が雨) }{Prob(4/2が雨)} }

ベイズの定理を使うコツ＝とにかく分解すること

f:id:graziegrazie:20171022133339p:plain
Fig. 事後確率の算出

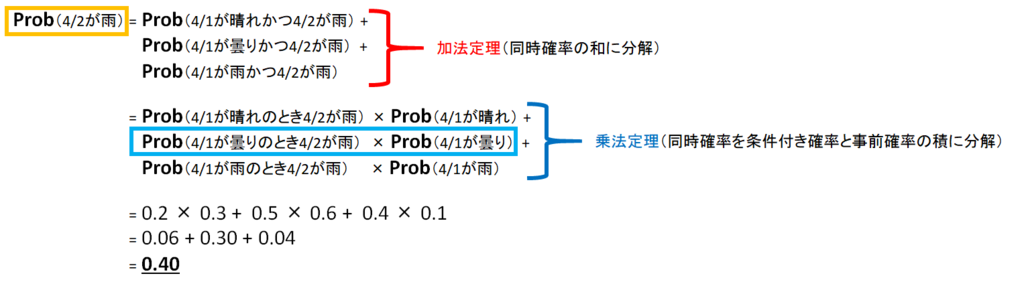
従って求める確率は
f:id:graziegrazie:20171022134050p:plain
となる。分母の値（データが得られる確率）が直接与えられない場合は、このようにして求める。


Table. Likelihood
4/1が晴れの時に4/2が雨の確率 0.2
4/1が曇りの時に4/2が雨の確率 0.5
4/1が雨の時に4/2が雨の確率 0.4

Table. Prior Probability
4/1が晴れ 0.3
4/1が曇り 0.6
4/1が雨 0.1

理由不十分の原則

　確かな情報がない場合は、適当な値をセットできる

ベイズ更新

　新旧データ或る時に、旧データから得られた事後確率を新データの事前確率として利用すること

例題2.

ケンの彼女Ｋ子がケンを好きな確率は？

この問題では、心を確率モデル化してみる。心には２種類の因子があり、それらを「愛」・「憎」とする。このとき、

Table. Probabilistic model of K子's feeling
K子の心情 嫌い ふつう 好き
愛
1
2
3
憎
3
2
1

デートの印象が悪い　→　「憎」が引かれた
デートの印象が良い　→　「愛」が引かれた
＊引かれた「愛」・「憎」は元に戻る。つまりそれぞれの感情において、「愛」・「憎」の数は常に一定とする。

最近２回のデートの印象は、順に「良」・「悪」であったとする。

１回目のデートで良を得る確率

Ｄ＝１回目のデートで良を引く
Ｈ＝Ｋ子がケンを好き

{ Prob(デートの印象「良」が「好き」から生まれた） = \frac{Prob(「好き」の時に「良」を引く) \times Prob(「好き」)}{Prob(「良」を引く確率)} }


Table. Likelihood
嫌い ふつう 好き
「良」を得る確率 1/4 2/4 3/4
「悪」を得る確率 3/4 2/4 1/4

Table. Prior Probability from Ken's inspiration
嫌い ふつう 好き
0.1 0.3 0.6

Ｋ子がケンのことが好きかの事前情報はないので、理由不十分の原則から「好き」・「ふつう」・「嫌い」は各1/3の確率とするのが一般的である。しかしケンはＫ子と直に接していることから、ケンの実感を採用することが出来る。これは明確な根拠がないため、各心情である確率をを1/3するよりもケンの経験を根拠にしていることから、精度は高そうである（勿論本人が勘違いをしている可能性は捨てきれないが。。。）。このようにベイズ確率では、経験のような根拠の薄い情報を考慮できるという柔軟さがある。

その結果、

f:id:graziegrazie:20171022174438p:plain
Fig. Prob（良）の算出
となる。次に１回目を踏まえた２回目の結果を求める。

事前準備

１回目のデートの結果を踏まえ、

  • {\displaystyle Prob（「良」が「ふつう」から引かれた）}
  • {\displaystyle Prob（「良」が「嫌い」から引かれた）}

をそれぞれ求める。結果は、

Table. Prior Probability from Ken's inspiration
嫌い ふつう 好き
0.04 0.24 0.72

{ \displaystyle Prob(デートの印象「悪」が「好き」から生まれた） = \frac{Prob(「好き」の時に「悪」を引く) \times Prob(「好き」)}{Prob(「悪」を引く確率)} }

f:id:graziegrazie:20171022180151p:plain
Fig. ２回目のデートの結果としてProb（「悪」を引く）の算出

よって２回のデートの結果、Ｋ子がケンに対して抱いている感情は、
{ \displaystyle Prob(デートの印象「悪」が「好き」から引かれた） = \frac{\frac{1}{4} \times 0.72}{0.33} \simeq 0.55 \\ \displaystyle Prob(デートの印象「悪」が「ふつう」から引かれた） = \frac{\frac{2}{4} \times 0.24}{0.33} \simeq 0.16 \\ \displaystyle Prob(デートの印象「悪」が「嫌い」から引かれた） = \frac{\frac{3}{4} \times 0.04}{0.33} \simeq 0.09 }

確率分布

例題3.

表の出る確率が{\theta}のコインがあり、３回投げると

  • １回目　表
  • ２回目　表
  • ３回目　裏

と出た。この時{\theta}の確率分布を求めよ。

この場合、データは「表」が出ること、仮説は「表」の出る確率が{\theta}となる。よって求める確率は、
{ Prob(「表」が出た時に「表」が出る確率が\thetaである）= \frac{Prob(「表」が出る確率が\theta) \times Prob(\thetaが成立する) }{Prob(「表」が出た)} }
ここで"「表」の出る確率が{\theta}"という文言を"{\theta}のコイン"と置き換えると、上記は
{ \frac{Prob(\thetaのコインで「表」が出る) \times Prob(\thetaのコインが存在する)}{Prob(「表」が出た)} }

ベイズの定理の左辺は原因が発生する確率
{Prob(「表」が出た)}は定数のため{C}と置く

  • 尤度　　：{Prob(\thetaのコインで表が出る \ = \ \theta}
  • 事前確率：1(理由不十分の原則)

よって
{ Prob(「表」が出た時に「表」が出る確率が\thetaである） \ = \ \frac{\theta times 1}{C_1} }
となる。
{ \displaystyle \int f(\theta) d \theta = 1 }
より、{\displaystyle C_1 \ = \ \frac{1}{2}}
{\displaystyle f_1(\theta) \ = \ 2 \theta}
となる。２回目の事後分布は、
{ \displaystyle Prob(「表」が「\thetaのコイン」から出た) \\ \displaystyle = \frac{Prob(「\thetaのコイン」から表が出る) \ \times \ Prob(「\thetaのコイン」の存在確率)}{Prob(「表」が出る)} \\ \displaystyle = \frac{尤度\theta \times １回目の事後分布2\theta}{定数C_2} }
１回目と同様にして{\displaystyle C_2 \ = \ \frac{2}{3}}, \ f_2(\theta) \ = \ 3 \theta^2となる。３回目は裏が出たので、
{ \displaystyle Prob(「裏」が「\thetaのコイン」から出た) \\ \displaystyle = \frac{Prob(「\thetaのコイン」から裏が出る) \ \times \ Prob(「\thetaのコイン」の存在確率)}{Prob(「裏」が出る)} \\ \displaystyle = \frac{尤度(1 \ - \ \theta) \times ２回目の事後分布3\theta^2}{定数C_3} }
であり、{\displaystyle f_3(\theta) \ = \ 12(1 \ - \ \theta)\theta^2}

＊参考文献

「頻度論」の学者と「ベイズ論」の学者が対談したら | 『統計学が最強の学問である［実践編］』発刊記念対談 | ダイヤモンド・オンライン

NVIDIA製GPU搭載のハイスペックノートPCを探してみた

画像処理などをリアルタイムで行いたい場合、CPUはもちろん、ハイスペックなGPUが搭載されているとストレスがないです。またDeep Learningなどの機械学習を行う場合、OSSのライブラリはCUDAが必要なことが多い気がします。CUDAのインストールには、NVIDIA性のGPUが必要です。そこでNVIDIA製GPUを搭載可能なハイスペックノートPCを探してみました。

探索条件

・メーカ：Lenovo, HP, Microsoft, マウスコンピュータ
・ＣＰＵ: core i7
・メモリ：20GB以上
・サイズ：13～14インチ（持ち運び製を考慮して)
・重量：1.5kg以下

結論としては、個人的に好きなLenovo、そしてHPは上記の条件を満たすPCはなかったです。Surfaceとマウスコンピュータがいい感じでした。Surfaceの方がデザインが好きなのですが、いかんせん高いのがたまにキズ。。。

探索結果

Lenovo（2017/10/21現在)

  • Tシリーズ

T470s　　 ：NVIDIA製GPU非対応
ThinkPad25：売り切れ

  • Aシリーズ

NVIDIA製GPU非対応

  • ゲーミングPC

サイズ超過

HP（2017/10/21現在)

一般PC　　　：希望条件を満たすPCなし
プレミアムPC：NVIDIA製GPU非対応

Microsoft（2017/10/21現在)

Surface book2 ：全条件を満たした！
Surface Laptop：NVIDIA製GPU非対応
Surface Pro　 ：NVIDIA製GPU非対応

マウスコンピュータ（2017/10/21現在)

G-Tune NEXTGEAR-NOTE i4400 シリーズ：全条件を満たした！
DAIV-NG4500シリーズ　　　　　　　　：全条件を満たした！
LuvBook J シリーズ：NVIDIA製GPU非対応