Probabilistic Robotics - Chap.6 Robot Perception

1.Introduction
６章に記載されているのはEnvironment Measurement Model（環境計測モデル）
確率ロボティクスではセンサデータの計測に伴うノイズもモデル化する

${ \displaystyle p(z_t | x_t, m) \\ z_t：時刻tでのセンサデータ\\ x_t：時刻tでのロボットの位置\\ m：環境地図 }$

確率ロボティクスでは、センサモデルの不正確さに対し、統計的手法を用いて対応する

${ \displaystyle z_t = \{z^1_t, ..., z^K_t\} z^k_t:センサAが時刻tにおいて計測した個々のデータ（LRFならば角度\thetaにおける距離） }$

${ \displaystyle p(z_t | x_t, m) = \prod_{ k = 0 }^K p(z^k_t | x_t, m) }$
この式は、 ${p^k_t}$ がそれぞれ独立していることを仮定しているが、理想状態でしかそれはありえない。

6.2 Maps

地図 ${m}$ はオブジェクトのリストを表す
${\displaystyle m = \{m_1, ... , m_N\} }$

地図には２種類ある

特徴ベース：オブジェクトの位置は地図中に含まれている。形状情報のみ特徴として持つ。そのため、ロボット用のマップとしてはこちらの形式がよく使われる。
位置ベース： ${m}$ の要素は環境中に存在するオブジェクトの位置を表す。各オブジェクトの位置をデータとして保つ必要があるので、データサイズが大きい。空きスペースに関しての情報も保つ必要がある、つまり全セルの情報を保つ必要がある。

6.3 Beam Models of Range Finders

Range Finderは最もよく使われるセンサ

6.3.1 The Basic Measurement Algorithm

ここで紹介するモデルは４つのエラーを考慮する

分解能によって生じる誤差

正しい距離は計測できているものの、分解能の制約により誤差が乗る場合がある。
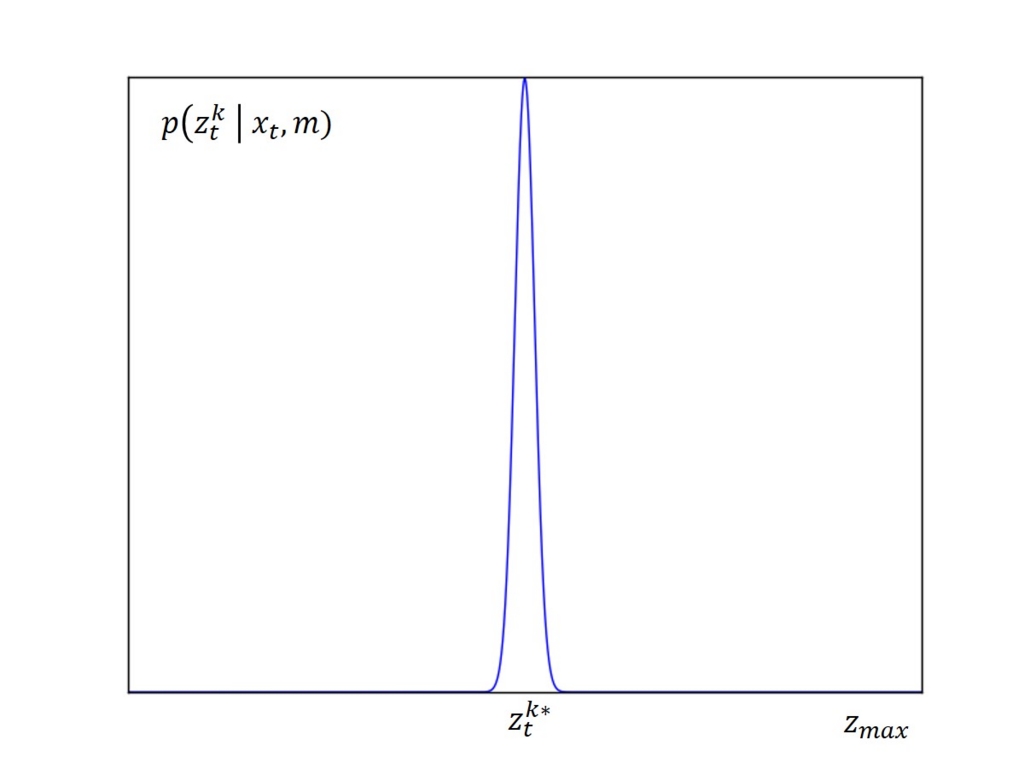
正しい距離を ${z^{k*}_t}$ とする
本計測誤差は、平均 ${z^{k*}_t}$ 、分散 ${\sigma_{hit}}$ で表される狭いガウス分布でモデル化できる。
${\sigma_{hit}}$ は本ノイズモデル固有のパラメータ

f:id:graziegrazie:20170405202747j:plain

予想外の物体

環境地図に元々含まれていない物体は、元々の地図に記載していたよりも短い距離で見つかることある
尤度は物体との距離に応じて減少していくことから、指数分布で表される。
この指数分布はモデル固有のパラメータ ${\lambda_{short}}$ を使って表せる。

${ \begin{eqnarray} p_{short}(z^k_t|x_t,m) = \begin{cases} \eta \lambda_{short} e^{-\lambda_{short} z^k_t} if 0 \gt z^k_t \gt z^{k*}_t \\ 0 otherwise \end{cases} \end{eqnarray} }$

指数分布は自らの位置から本来の対象の位置までの尤度を表すため、累積確率は

計測失敗

計測可能レンジの超過
つまり計測値は最大値を示す

ランダム計測

ごくたまに起きる説明の使いない計測結果

それぞれのエラーの密度関数は、それぞれ重みを掛けて合体することで、本モデルの確率密度関数を表現できる

Limitation of the Beam Model

Beamモデルには２つの主な欠点がある
滑らかさがない
　椅子を検知したら椅子の足それぞれマッピングするかもしれない
　ロボットの位置が変化したら、beamの座標変換の計算量が大変なことになる
滑らかさの欠如は２つの問題を招く
　beliefの近似が正しい状態を見失いやすい
　山登り法は局所最大値に陥りやすい
計算量が膨大

4 Liklihood Fields for Range Finders

6.3の制限を解決する尤度フィールドモデルについて述べる。
確率計算などはしないが、実際に使ってみると良い結果が求まる、アドホックなアルゴリズム。

キーとなるアイデアは、 ${z_t}$ の端点をグローバルマップ上に投影すること。
これにより、グローバルマップとロボットのローカルマップの位置関係がわかる。
投影される端点の座標は、
${ \left( \begin{array}{ccc} x_{z^k_t} \\ y_{z^k_t} \end{array} \right) = \left( \begin{array}{ccc} x \\ y \end{array} \right) + \left( \begin{array}{ccc} cos \theta & -sin \theta \\ sin \theta & cos \theta \end{array} \right) \left( \begin{array}{ccc} x_{k,sens} \\ y_{k,sens} \end{array} \right) + z^k_t \left( \begin{array}{ccc} cos \left(\theta + {\theta}_{k,sens} \right) \\ sin \left(\theta + {\theta}_{k,sens} \right) \end{array} \right) \tag{6.32} }$
として表される。
このとき、 ${ x_t = \left( \begin{array}{ccc} x & y & \theta \end{array} \right)^T }$ はロボットの座標、
${ \left( \begin{array}{ccc} x_{k,sens} & y_{k,sens} \end{array} \right)^T }$
はセンサ検出データの端点
をそれぞれ示す。

Beam Modelと同様に、こちらは３種類のノイズを定義

計測ノイズ

　計測過程で起こる、ガウス分布でモデル化されるノイズ

計測失敗

　センサの最大計測可能距離の時を指す。その時、値が正しいかは不明。

説明の付かない計測結果

　ランダムに発生するノイズ

5 Correlation-Based Measurement Models

文献でよく見かけるmap matchingを使うモデル。
map matchingは、連続するスキャンデータをローカルマップへ落とし込む
つまりmap matchingは、グローバルマップを ${m}$ 、ローカルマップを ${m_{local}}$ とした時、尤度 ${p\left(m_{local} | x_t, m \right)}$ が高い場所を探すことを指す

尤度は、
${ p\left(m_{local} | x_t , m \right) = max \left\{ {\rho}_{m , m_{local} , x_t} , 0 \right\} }$
で表され、グローバルマップとローカルマップの相関係数 ${{\rho}_{m , m_{local} , x_t}}$ と平均地図 ${\overline{m}}$ はそれぞれ、
${ \rho_{m , m_{local} , x_t} = \frac { \sum_{x, y} \left(m_{x, y} - \overline{m} \right) \left( m_{x, y, local} \left( x_t \right) - \overline{m} \right) } { \sqrt {\sum_{x, y} \left(m_{x, y} - \overline{m} \right)^2 \sum_{x, y} \left( m_{x, y, local} \left( x_t \right) - \overline{m} \right)^2 } } }$
${ \overline{m} = \frac{1}{2N} \sum_{x, y} \left( m_{x, y} + m_{x, y, local} \right) }$
尤度フィールドに対するmap matchingの利点は、相関係数に応じてフリースペースを決めること。これにより、センサの計測範囲外のデータも考慮してマップを作ることができる
一方map matchingの欠点は、物理的に明確な説明ができないこと

Feature-Based Measurement Model

今まではセンサの生値をベースとした話
これは一歩進んだ、センサデータから求めた特徴量をベースとした話
Featureベースの利点は、特徴量を低次元化することで計算量の削減が可能な点

ロボットの世界では、環境中の特徴量はランドマークと呼ぶことが一般的
特徴量を求める時に一般的なのは、センサがセンサを基準としたランドマークとの距離と方角を計測できるとする仮定
加えて、特徴量抽出器はサイン（本書では数値で表されるとする）を出力する可能性がある

特徴量ベクトル ${f}$ は、距離 ${r}$ と方角 ${\phi}$ 、サイン ${s}$ それぞれを使って
${ f \left( z_t \right) = \left\{ f^1_t, f^2_t, ... \right\} = \left\{ \left( \begin{array}{ccc} r^1_t \\ \phi^1_t \\ s^1_t \end{array} \right) , \left( \begin{array}{ccc} r^2_t \\ \phi^2_t \\ s^2_t \end{array} \right) ,... \right\} }$

確率ロボティクスのアルゴリズムでは下記の条件付き確率を仮定する
${ \displaystyle p \left( f \left( z_t \right) | x_t, m\right) = \prod_i p(r^i_t, \phi^i_t, s^i_t | x_t, m) }$

特徴量ベース地図に向けたセンサモデルの改定
特徴量の地図上での位置を ${m_i}$ とし、ロボットの座標を ${ \left( \begin{array}{ccc} x \ \ y \ \ \theta \end{array}\right)^T }$ とすると、特徴量の位置は
${ \left( \begin{array}{ccc} r^i_t \\ \phi^i_t \\ s^i_t \end{array} \right) = \left( \begin{array}{ccc} \sqrt{ \left( m_{j, x} - x \right)^2 + \left(m_{j, y} - y \right)^2 } \\ atan2 \left( m_{j, y} - y, m_{j, x} - x \right) - \theta \\ s_j \end{array} \right) + \left( \begin{array}{ccc} \epsilon_{\sigma^2_r} \\ \epsilon_{\sigma^2_\phi} \\ \epsilon_{\sigma^2_s} \end{array} \right) }$
ここで ${\epsilon_{\sigma^2_r}と\epsilon_{\sigma^2_r}, \epsilon_{\sigma^2_r}}$ は、平均０で、分散がそれぞれ ${\sigma_r, \sigma_\phi, \sigma_s}$ のガウシアン誤差変数

距離・角度センサの主要な問題点は、データの関連付けである。
これを解決するために ${f^i_t}$ と ${m_j}$ の間の一致変数 ${c}$ を導入する
${c_i = j \leq N}$ の時、 ${i}$ 番目の特徴量は ${j}$ 番目のランドマークと一致する
${N}$ はランドマークの総量

Sampling Poses

今までは特徴量の確からしさについて議論してきた
一方で、特徴量と地図情報からロボットの座標を推定したい時もある
そのためには、事前確率 ${p \left( x_t | c^i_t, m \right)}$ が必要である。
あり得ないが事前確率を均一分布とするとロボットの座標の尤度は
${ p \left( x_t | f^i_t, c^i_t, m \right) = \eta \ p \left( f^i_t | c^i_t, x_t, m \right) p \left( x_t | c^i_t, m \right) \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = \eta \ p \left( f^i_t | c^i_t, x_t, m \right) }$